sebadorn.de

Ein Artikel darüber, wie man herausfindet, ob ein Punkt (von einem Mausklick) innerhalb einer bestimmten geometrischen Form (hier: einer Ellipse) liegt, diese sich aber nicht im Koordinaten-Ursprung befinden und noch dazu rotiert wurden.

Das Ziel

Auf einer <canvas>-Fläche befinden sich mehrere Figuren. Klickt man auf die Fläche, soll die getroffene Figur ausgewählt werden. Die Figuren können sich sonstwo befinden und wurden unter Umständen auch rotiert.

Das Ellipsen-Objekt

Zum Zeichnen eines Ellipsen-Objektes werden ein paar Informationen benötigt. Dies sind meine Variablennamen und ihre Bedeutung:

x, y, width, height

Geben die Position auf dem Canvas und Breite/Höhe an.

rotate

Rotationswinkel, der angewendet werden soll. Als Einheit werden Rad verwendet (360° = 2π rad).

ctx

Der 2D-Kontext des Canvas, dessen Funktionen zum Zeichen verwendet werden.

Zeichnen der Ellipse

Der folgende Code stammt von Web Reflection: ellipse and circle for canvas 2d context.

draw: function() {
	var hB = ( this.width / 2 ) * .5522848,
		vB = ( this.height / 2 ) * .5522848,
		eX = this.x + this.width,
		eY = this.y + this.height,
		mX = this.x + this.width / 2,
		mY = this.y + this.height / 2;

	this.applyRotation();

	this.ctx.beginPath();
	this.ctx.moveTo( this.x, mY );
	this.ctx.bezierCurveTo( this.x, mY - vB, mX - hB, this.y, mX, this.y );
	this.ctx.bezierCurveTo( mX + hB, this.y, eX, mY - vB, eX, mY );
	this.ctx.bezierCurveTo( eX, mY + vB, mX + hB, eY, mX, eY );
	this.ctx.bezierCurveTo( mX - hB, eY, this.x, mY + vB, this.x, mY );
	this.ctx.closePath();

	this.ctx.fill();
}

Die Rotation wende ich in einer eigenen Funktion auf den Canvas-Kontext selbst an. Damit sich die Ellipse dabei nicht verschiebt, muss ihr Mittelpunkt zuerst in den Koordinaten­ursprung verschoben werden mit translate(x, y). Danach wird sie rotiert und wieder an ihre vorherige Position gesetzt.

applyRotation: function() {
	if( this.rotate != 0 ) {
		var xShift = this.x + parseInt( this.width / 2 ),
			yShift = this.y + parseInt( this.height / 2 );

		this.ctx.translate( xShift, yShift );
		this.ctx.rotate( this.rotate );
		this.ctx.translate( -xShift, -yShift );
	}
}

Wundert sich schon jemand, warum erst nach (xShift, yShift) und später nach (-xShit, -yShift) verschoben wird? Von der Logik her muss es natürlich andersherum sein und so geschieht es intern auch. Bei Funktionen wie translate() und rotate() werden entsprechend Matrizen multipliziert. Eine Besonderheit bei der Matrizenmultiplikation ist es, dass die Faktoren in umgekehrter Reihenfolge aufgelistet werden müssen, als sie dann Anwendung finden.

Liegt der Punkt innerhalb?

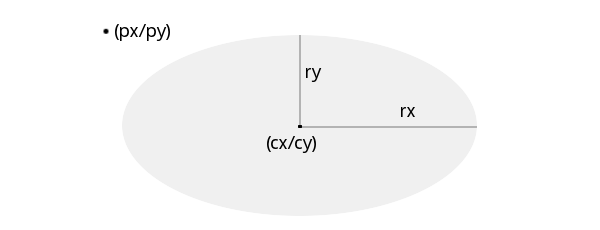
Nach einigen vergeblichen Suchen und Versuchen stieß ich auf die passende mathematische Formel (Quelle). Sei (px, py) die Koordinate des Klicks, (cx, cy) der Mittelpunkt der Ellipse und rx und ry der Radius auf der entsprechenden Achse. Hier ist keine Rotation berücksichtigt! Dann gilt für einen Punkt (px, py) innerhalb der Ellipse:

(px - cx)² / rx² + (py - cy)² / ry² <= 1

Das implementieren wir nun in einer Funktion. Wie gesagt, Rotation wird dabei noch nicht berücksichtigt, sehr wohl aber Verschiebung.

posInside: function( px, py ) {
	var wh = this.width / 2,
		hh = this.height / 2,
		cx = this.x + wh,
		cy = this.y + hh;

	var rotatedCoord = this.rotateCoordinate( px, py );
	px = rotatedCoord.px;
	py = rotatedCoord.py;

	var part1 = Math.pow( ( px - cx ) / wh, 2 ),
		part2 = Math.pow( ( py - cy ) / hh, 2 );

	if( part1 + part2 <= 1 ) {
		return true;
	}

	return false;
}

Rotation der Klick-Koordinate

Um die Rotation der Ellipse noch mit einzubeziehen, bin ich hergangen und habe den Klick-Punkt um den Mittelpunkt der Ellipse in gleichem Maße wie die Ellipse selbst rotiert. Die Formel (Quelle) lautet:

px = cx + (px - cx) * cos(-α) - (py - cy) * sin(-α)
py = cy + (px - cx) * sin(-α) + (py - cy) * cos(-α)

Dabei ist α die Rotation des Elementes in rad. Der Wert ist negativ, da in der Formel und dem Code zuvor von einer unrotierten Ellipse ausgegangen wurde – was eine Rotation zurück in die Ursprungslage bedeutet.

rotateCoordinate: function( px, py ) {
	if( this.rotate != 0 ) {
		var cx = this.x + this.width / 2,
			cy = this.y + this.height / 2,
			px_translate = px - cx,
			py_translate = py - cy,
			rotateCos = Math.cos( -this.rotate ),
			rotateSin = Math.sin( -this.rotate );

		px = cx + px_translate * rotateCos - py_translate * rotateSin,
		py = cy + px_translate * rotateSin + py_translate * rotateCos;
	}

	return { px: px, py: py };
}

Das war es.